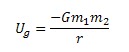Waterproof Electricity

Researchers at Oxford University proudly announced the development and successful testing of a new material which will conduct electricity even when underwater. The so-called 'waterproof electricity' is the result of a new type of plastic which will conduct an electric current but prevents any "leakage" of electric charges into the water.  Their findings, published in Materials Journal, mark a significant point in global materials development.

Historically, water has always been the biggest enemy of electrical devices. The only way to protect devices which are to be used underwater has been to physically coat them in a waterproof and airtight layer, leading to cumbersome and clunky devices, and as they to be operated underwater, this additional layer has made them particularly difficult to use.

Professor David Armstrong, the team leader at Oxford, explained, "As per recent information, we have been able to conduct electricity through our new material without any loss of current to the surrounding water. Clearly this opens up all kinds of applications, from underwater research to making domestic mobile devices waterproof." 

Dr Emily Turner, a senior researcher on the team, added, "The potential for this material is immense. We are looking at applications in underwater robotics, marine exploration, and even in everyday consumer electronics. The ability to have devices that are both electrically conductive and waterproof could revolutionize many industries."

Professor Mauro Pasta, another key researcher, emphasized the collaborative effort: "This project has been a true interdisciplinary endeavor, combining expertise from materials science, chemistry, and electrical engineering. The synergy between these fields has been crucial in achieving this breakthrough."

The research for the new polymer is based on PTFE (Teflon) which is water resistant, while having additional atom chains which enable it to conduct electricity.  Known as Fluoro-Ortho-Oxy Limonene, it's a highly oxygenated organic molecule formed from the oxidation of limonene. It features a unique structure that includes both closed-shell and open-shell peroxy radicals, which contribute to its exceptional properties.  Part of its structure is shown below. Its full chemical structure and further details will be released in an online article at noon today.

If you'd like to read more of my Chemistry articles, I can recommend my explanation of how I got into online A/B testing as a Chemistry graduate.

If this sounds like something out of Star Trek, there's probably a good reason for it.  

Can a 747 take off from a conveyor belt runway?

This question is currently going round on Facebook; one of my friends posted it, I answered it, and a few hours later entered a lengthy and circular debate in the comments section.  Here, with more space than a Facebook comments section, I'd like to pose the question, answer it and then address some of the misconceptions.

Here's the question:  Imagine a 747 is sitting on a conveyor belt, as wide and long as a runway.  The conveyor belt is design to exactly match the speed of the wheels, moving in the opposite drection.  Can the plane take off?

Shared originally by Aviwxchasers.Com a news and media site from the US.

My friend shared the post, and answered, "No - there's no way to generate lift."
My original answer:  

"I think you're assuming that the 747 will be moving because its wheels are being driven. The forward thrust of the aircraft comes from its engines, not from making its wheels turn (like a car). So the engines push the aircraft forward and the wheels just slide and skid along the conveyor belt , while the engines push the aircraft to take-off speed. The wheels don't have to turn to allow the aircraft to move."

However, this wasn't deemed sufficient by some other commentators, who (to summarise) posted the following questions or objections.

1. The conveyer would counteract the forward movement produced by the engines' thrust.  The conveyor matches the speed of the wheels in the opposite direction, so there can be no forward motion.
2. Lift is created by air flow over the wings. It doesn't matter how much thrust you have , if doesn't generate airflow over the wing, it won't fly.
3. The method of propulsion should be irrelevant. If the speed of the conveyor matches the speed of the wheels in the opposite direction, there can be no forward motion.
4. Take the vehicle out of the equation, it's all about the wheels and the conveyor. The faster the wheels turn, the faster the conveyor goes. Stick anything you want on top of the wheels, the principles are the same. Newton's third law
5. Indeed it's not about the wheels it's about forward movement (thrust from the engine) needed to take off but that forward movement is being counteracted by the conveyer    

Here, I propose to look at these arguments individually and collectively, and explain why the points which are raised aren't sufficient to stop the aircraft from moving and taking off.

1.  The conveyor would counteract the forward movement produced by the engines' thrust.  The conveyoy matches the speed of the wheels in the opposite direction, so there can be no forward motion.

1A.  The conveyor will only stop the wheels' rotation from generating forward movement.  However, it is not the wheels which are being driven - this is not a car or a truck.  The forward movement of the plane is not a result of the wheels successfully pushing against the conveyor belt; the forward movement of the plane comes from the push of the engines.  The result is that the plane will move forwards (the engine pushes against the air flowing through it, the air pushes back - Newton's Third Law) and the wheels will spin and skid down the track.

It's not "The plane moves forwards because the wheels go round", it's, "The wheels go round because the plane goes forwards [over a surface which has sufficient friction] ."


2. Lift is created by air flow over the wings. It doesn't matter how much thrust you have , if doesn't generate airflow over the wing, it won't fly.

True.  But there is thrust, and it is generating airflow over the wing.  The conveyor belt does not have the ability to resist the movement of the plane, only to counteract the turning of the wheels.  

The plane can move forwards -even along the ground - without its wheels turning.  The engine isn't driving the wheels.

3.  The method of propulsion should be irrelevant. If the speed of the conveyor matches the speed of the wheels in the opposite direction, there can be no forward motion.
and 
4. Take the vehicle out of the equation, it's all about the wheels and the conveyor. The faster the wheels turn, the faster the conveyor goes. Stick anything you want on top of the wheels, the principles are the same. Newton's third law

3A and 4A.  Comment 3 was a response to my question, "What happens if we replace the 747 with a space rocket, aligned horizontally on the conveyor belt runway, on wheels?"  and the comment suggests a misunderstanding about what's causing the forward motion of the plane.  The thrust of a space rocket is completely independent of the any wheels (they normally fly fine without them) and the wheels will just get dragged along the conveyor belt, without turning. 

Yes, the faster the wheels turn, the faster the conveyor belt goes.  But the wheels don't have to turn for the plane to move (as I said in response to 2).  The conveyor belt does not have some property which prevents something from skidding along it, just from preventing any forward motion due to wheels turning on it. 

You can only take the vehicle out of the equation when you realise that the vehicle isn't a car, with the limitations that a car has.

Newton's third law applies to rotating wheels and conveyor belts.  It also applies to the aircraft engines and the air flowing through them, or to space rockets and the fuel burning inside them.  I wonder if the Starship Enterprise (on wheels) would have this problem?

5.  It's all about forward movement (thrust from the engine) needed to take off but that forward movement is being counteracted by the conveyer  

The forward movement is not counteracted by the conveyor.  The conveyor just stops rotating wheels from generating any forward movement.  But if the wheels aren't rotating (because they're not being driven, such as in a car) then there's no movement to resist.

In conclusion, I'd like to offer this video from "Mythbusters" which shows a light aircraft attempting to take off against a conveyor belt (which in this case is being pulled by a pickup truck to match the plane's speed).  To quote one of the engineers, "People just can't wrap their heads around the fact that the plane's engine drives the propellor, not the wheels."

Some other 'everyday maths' articles I've written:

A spreadsheet solution - the nearest point to the Red Arrows' flight path from my house
The Twelve Days of Christmas - summing triangle and square numbers
Why are manhole lids usually circular?
"BODMAS" puzzles - what's the fuss?

Physics: The Sound Barrier and Sonic Booms

After sobering up from his drunken walk home, Isaac Newton went to see his friend, Mr Science.  However, as Isaac went along, he noticed that the roadway to Mr Science's house was very busy; Mr Science lived in the middle of town, and it was market day, and Isaac found that there were large crowds of people milling around in front of him.  Still, walking was definitely the quickest way to see his friend, as although gravity had been invented, cars were still some way off in the future.

Isaac Newton was quite keen to get to Mr Science's house to discuss his adventures with apples, including his failed attempt to launch it into space, and started jogging and jostling through the crowd, shouting at people to move out of the way, instead of just meandering through it.  He bumped into people more frequently as he did so, but kept on jogging undeterred, and found that the faster he jogged, the more people he bumped into; in the end, he put his arms out in front of him like a wedge and started pushing his way through with more effort.  This continued until he found that crowds of people were gathering together in front of him, despite him shouting at them, they were barely unable to get out of his way before he started ploughing into them.  Finally, he realised he was going that fast, that the people, all bunched up in front him and desperate to get out of his way, were unable to stand aside and he sent the crowds tumbling left and right in front of him.

When he arrived at Mr Science's house, he recounted the strange behaviour of the crowd and the various stages he'd encountered. "That's interesting," commented Mr Science, "That reminds me of an experiment I've just been running."

Isaac's journey through the crowd is very similar to an aircraft (or a car) as it travels at speeds close to the speed of sound.  The atmosphere is made up of gas particles which travel around, silently bouncing off each other and generally behaving randomly (in the real sense of the word), at speeds which are close to - but less than - the speed of sound.  Particles in a gas are extremely small (as all particles are), and by comparison, the spaces between them are relatively large.  This means that there are large gaps between them, and if you move a large, solid object between them (or, for example, start walking through them) then you're able to push them aside and move through the gas.  

Walking at low speeds, you're not likely to notice this effect, but at larger speeds, for example running, you'll feel the air as it rushes past your face.  Cycling through the air, you'll feel this more strongly, and as you increase your speed, you'll begin to feel the effort of pushing through the air - it'll feel as if there's a wind blowing into you, pushing you back.  This is known as 'air resistance' and it increases as your speed increases.  You're pushing more and more air particles aside, as you cut through the air, and this takes more effort.  At these speeds, it becomes more and more important to get into an aerodynamic position - as low down as possible, elbows tucked in, and so on, to cut through the air as economically and as easily as possible.  In Isaac Newton's case, he put his arms out in front of him like a wedge, so that he could push through the crowds of people as easily as possible.

Now, the gas particles in the atmosphere are bouncing around, flying around at close to (but less than) the speed of sound, which is 330 metres per second (or thereabouts).  In an aircraft, it's possible to approach and exceed the speed of sound, but in order to do so, the aircraft has to push through the air particles as if they were a crowd.  At walking and cycling speeds, the air particles can easily move aside as you push through them, but at speeds close to the speed of sound, they particles are unable to get out of the way of an aircraft.  The aircraft has to shove the particles aside - this becomes very difficult at speeds close to the speed of sound - and break through the sound barrier.  

The air particles start to bunch up in front of the nose of the aircraft until eventually (if it continues to accelerate) they are pushed aside in a huge compression wave.  All these particles pushed together in one go produce a loud noise - a sonic boom - as the aircraft exceeds the speed of sound and goes supersonic.  

 This sonic boom continues to travel along the ground and will be heard along the line of the aircraft's flight path - it isn't produced just once and then stops.  Mr Science tried to explain all this to Isaac, but Isaac was extremely pleased with having discovered gravity, and wasn't in the mood to discuss ways of beating it in huge flying machines, let alone ones that could travel faster than sound.  "Maybe some other time," he explained to his friend, "When I've finished with the apples."

If you find this post helpful, you may also be interested in:

Calculating the packing density of closely-packed spheres
Calculating the packing density of closely-packed circles
Calculating the tetrahedral bond angle

Physics: Gravity vs Sound

Isaac Newton, upset with his failed attempt to discard the apple that woke him from his afternoon nap, decided that it was time to take stronger measures to destroy the apple once and for all.  Deciding that he would give the stupid apple a lesson in gravity, he took it to the top of a tall building, and dropped it, so that it would hit the ground at great speed and disintegrate into lots of tiny pieces of apple sauce.

However, to his horror, he realised at the exact moment that he dropped the apple that there was a poor unfortunate man standing directly underneat the apple, and shouted down at the man to move out of the way of the doomed fruit.

But would the man hear Isaac's shout in time?  Or would he suffer the same fate as our unfortunate father of modern physics?

The question is - which will reach the man first:  the apple, accelerating due to gravity, or the sound of Mr Newton's shout, travelling at the constant speed of sound?

Firstly, the apple.  The apple is accelerating at 9.81 ms^-2, getting faster all the time.  Yes, I'm ignoring terminal velocity and air resistance for now.

The formula to use for the apple is   s = ut + 1/2 a t².
s = distance travelled
u = initial velocity = 0
t = time since apple was dropped
a = acceleration due to gravity

since u = 0, (when the apple was dropped it had zero initial speed), we have a simplified formula:  s = 1/2 a t²
This tells us s (how far the apple has fallen) after so much time has passed (t).  We can rearrange it to tell us how long it will take the apple to fall from a building of height s.  This gives us:

√(2s/a) = t

The formula for the sound of Isaac Newton's shout is simpler:
v = s / t

s = distance
v = velocity = the speed of sound, 330 ms^-1
t = time since Isaac shouted

Rearranging gives us t = s / v

Now, suppose the building Isaac standing on was 300 m high, just short of the Chrysler Building's 319m.  No, the buildings in Isaac Newton's time weren't this tall, but let's just suppose he had a time machine and he made the journey.


For the apple: √ (2s/a) = t
Time taken is 7.82 seconds

And for the shout,

t = s / v = 300 m / 330 ms^-1 = 0.909 seconds


So, the shout will reach the ground (7.82 - 0.909 = 6.91) seconds before the apple does, giving the potential victim time to move out of the way.


From here, we can go on to work out how high a building would have to be for the apple and the sound to reach the ground at the same time. From any height above this, the apple would always land before the shout (because the apple will keep accelerating - we're still ignoring terminal velocity) and no amount of shouting would save a victim from being hit on the head by the apple.

In order to do the calculation, we simply set the time for the apple and the time for the shout to be equal.  This gives us:

t = √(2s/a) = s / v

√(2s/a) = s / v
2s/a = s² / v²

2 v² /a = s

We can now put in (substitute) the values for the speed of sound (330 ms^-1) and acceleration due to gravity (9.81 ms^-2), and calculate the height of the building (s).  


2 x 330² / 9.81 = 22,201 metres, whiich is very, very high indeed.  To put it another way:

It's just over 73,200 ft, which is 2.5 times higher than Mount Everest.
It's twice the height on airliner's cruising altitude.

Air resistance will be less of a problem to start with, but sound needs air to travel through, and the air is so thin at those heights that the sound won't travel as well or as fast.  I'm not even going to discuss the lack of air pressure; lack of breathable oxygen; the temperature (frozen apples and frostbite); terminal velocity and air resistance.

When, during an A-level class, my maths teacher posed this question, I don't think she was thinking of such things either.  That's the problem with maths without science - it can give you an answer that is meaningless and useless when you actually consider the real world!

Other Physics related articles you may find interesting:

Calculating the height of geostationary satellites
Calculating the angle of elevation of geostationary satellites
Calculating (and explaining) escape velocity

Measuring g using a pendulum

Physics discussion: Escape Velocity

The story goes that Isaac Newton was sitting under an apple tree, when an apple fell on his head, and prompted him to wonder why it fell downwards, and not upwards or even sideways.  However, what history doesn’t tell us is that he probably got quite upset at having his afternoon nap interrupted by an apple, and, in his annoyance, threw the apple away as far as he could, declaring, “Stupid apples!”  He then wondered why the apple fell back to the earth, despite him throwing it away as hard as he could.

The same applies today (gravity hasn't changed much since then).  Consider throwing a tennis ball:  the harder you throw it, the higher it goes.  How about throwing it upwards, or even aiming for the moon (it’s not a million miles away, you know)? How fast does it have to be travelling, or how quickly do I have to throw it, so that it doesn’t come back down again?  We call this initial speed (how fast you have to throw it) the escape velocity.

Thinking in scientific terms, we can say that the apple (or the tennis ball) has escaped from the Earth’s gravitational pull, and will not fall back down to the earth.  It has maximum gravitational potential energy, and no kinetic energy (i.e. it stopped moving).  This happens at the edge of the gravitational field.

Since the kinetic energy at the start (i.e. from the throw) has all been converted into potential energy, we can say that the two are equal.

The potential energy is:

And the kinetic energy is:

where m₂ is the mass of the object being thrown, and m₁ is the mass of the Earth. 

 I’ll explain a bit more here about how this works, because at school I was taught that gravitational potential energy = mgh¸ where m is mass, g is acceleration due to gravity, and h is height – so that potential energy continues to increase with height.  So, when does PE = mgh stop being correct?  PE = mgh is not true when h becomes large, and g becomes very small.  The value of g changes with height; close to surface of the earth, mgh is an acceptable approximation, however at high altitude, g becomes

very much smaller.  It’s different at the top of a mountain than it is at sea level for instance.

So, the definition of potential energy is something else, it’s not mgh, it’s taken as something else.PE for all locations is equal to the formula given above.

Since we can equate these two energies, we have that:

Solving for this revised equation gives an expression for escape velocity, v, as:

Where m₂ is the mass of the Earth (in this case) and r is the Earth’s radius from centre to surface (i.e. from the centre of gravity to the point we’re launching from), since we have a bit of a head-start on gravity (we don't have to launch from the centre of the Earth).

Solving for all the numbers gives us an escape velocity of 11,181 metres per second, which is 34 times the speed of sound (Mach 34).  If you tried to throw an object at this speed, you'd probably either break your arm, or suffer friction burns from the air resistance as the air particles tried to move out of the way of your arm (and failed).  

It's also worth mentioning that I've not looked at air resistance, which at Mach 34 is considerable.  The sonic boom caused by the apple (or the tennis ball) would be extremely loud... in fact, I imagine the apple would turn into apple sauce, and the tennis ball would melt into a sticky, furry goo before it got anywhere near earth orbit.

I should explain at this point that escape velocity isn’t the speed that space rockets travel at when they take off.  This is really important.

An important point about escape velocity

Remember at the start that we were talking about throwing objects – where all the energy, and force is transferred to the object at the start of its flight.  With space rockets, the engines keep pushing the space rocket while it’s in flight, so they don’t have to travel as quickly, they just have to push upwards with a force that constantly exceeds their weight until they achieve an earth orbit.  This means that space shuttles, and space rockets, don't have to reach escape velocity.  Instead, they just have to keep pushing upwards with a force that is greater than their weight, until they reach an orbital height.

Other astronomy related articles you may find interesting:

Calculating the height of geostationary satellites
Calculating the angle of elevation of geostationary satellites
The Earth-Moon distance is increasing (published 1 April 2011)
What are constellations?
Calculating (and explaining) escape velocity

Calculating the Earth-Moon distance

This post follows up my previous post on geostationary satellites.  Long before we were launching satellites (even non-geostationary ones), our natural satellite, the Moon, was orbiting the Earth.  As the moon goes around the earth, its phase (shape) changes, and in fact, the word "month" derives from "moonth", the time taken for the moon to go from new to full to new again.  This time is the time taken for one complete orbit around the Earth - the different phases of the moon are a result of us seeing a different amount of the lit half of the moon (I once based a very neat science lesson on this principle - in fact I used it in my interview lesson  and subsequently got the job).

One of my photographs of the moon, taken through a telescope.
The darkening at the bottom of the image is the edge of the
telescope's field of view

We can use physics, and our knowledge of the mass of the Earth, the value of pi and the time the Moon takes to complete one orbit, to work out how far it is from the Moon to the Earth.

Back to the two key equations that we'll need, which are the force on a body moving in a circular path:

where

And Newton's Law of Gravity

Equating the two, and rearranging to find r, gives us

This is the same equation used for geostationary satellites, and describes the basic relationship between the distance between two bodies (a planet and a moon, for example, or a star and a planet).  This gives it great power as it can be used in many different situations.

Turning to the current situation, then:

Calculation of the Earth-Moon distance:

G is the universal gravitational constant, 6.67300 × 10^-11 m³ kg^-1 s^-2

M is the mass of  the Earth, 5.9742 × 10²⁴ kg

T is the time to complete one orbit, which for the Moon is 27.32166 days, which is 2,360,591 seconds.

Plugging the numbers into the formula above gives the distance as 383,201 km

However, this is not the distance to the Moon from the Earth's surface.  Newton's law of gravity gives the distance between the centres of gravity of the two bodies.  I'm ignoring the radius of the Moon (which is perhaps an oversight on my part, you decide) but we must subtract the radius of the Earth from this value, to give the orbital height.  Radius of Earth = 6378.1 km, so the distance to the Moon is calculated as  = 376,823 km, or, if you prefer, (at 1.61 km to the mile), 234,147 miles.

Previously, I've learned that the Moon is about a quarter of a million miles away, so I'm glad the method I've used shows a figure which is 'about right' without any checking.  Looking at other sources, it looks like my figures are close enough, considering the assumptions I've made.  One key assumption I've made is to suggest that the moon travels in a circular orbit, and it doesn't.  It has an elliptical orbit, which means the distance from Earth to Moon changes during the orbit - so I've calculated an average distance.  Still, my figure is pretty close, and not a million miles away (and next time somebody reliably informs you that their opinion is not a million miles away, you can tell them that not even the Moon is that far away).

Other astronomy related articles you may find interesting:

Calculating the height of geostationary satellites
Calculating the angle of elevation of geostationary satellites
The Earth-Moon distance is increasing (published 1 April 2011)
What are constellations?

Calculating (and explaining) escape velocity
Measuring g using a pendulum