Maths Puzzle: How far does the fly fly?

Two boys set off on their bikes, at the same time, to meet each other.  They are 24 miles apart, and the road between them is perfectly straight.  The first boy cycles at 6 mph (he's only a very small boy), and the second boy cycles at 4 mph (because he's even smaller, and can't cycle as quickly).  A fly sets off from the first boy's handlebars at the same time as the boy starts cycling.  It flies in a straight line from the first boy's handlebars until it reaches the second boy's handlebars. It then turns around, and flies back to the first boy's bike, then when it reaches the first boy, it turns around again and back to the second boy's bike, and so on until the two boys meet.  The fly travels at 12 mph.


How far does the fly travel in total, from the moment the boys set off, until the moment they meet?  The time taken for the fly to turn around every time it reaches a boy can be ignored.


I like this type of puzzle - I liked it even more when I spotted an easy way of solving it. 


But first, the long way.

The fly sets off at 12 mph, at the same time as the second boy starts cycling towards it, at 4 mph.  There are 24 miles between them at this point, and the two travellers are approaching at 16 mph.  It will therefore take them


time = distance / speed = 24/16 = 1.5 hours


to meet.  This is the longest single part of the fly's journey, as the boys were at their furthest from each other.


However, in that time, the second boy has cycled 1.50 hrs x 4 mph = 6 miles, and the first boy has cycled 1.5hrs x 6 mph = 9 miles.
The fly has travelled 1.5 hours x 12 mph = 18 miles.  This makes sense - the second boy has cycled 6 miles, and the fly has travelled 18 miles, and 6 + 18 = 24 which was the starting distance between them.


Finally, while the fly has been flying the first leg of its journey, the two boys have reduced the distance between them from 40 miles to 24 - (9 + 6 miles) = 9 miles.

Now, the fly turns around, and starts to fly towards the first boy.  The first boy, remember, is cycling at 6 mph; the fly is still going at 12 mph, so their closing speed is 18 mph.  They have to travel 9 miles (the distance now remaining), so this will take:


time = distance / speed = 9 miles / 18 mph = 0.5 hours (which is 30 minutes).


In that time, the first boy travels 0.5 hours x 6 mph = 3 miles.
The second boy travels 0.5 hours x 4 mph = 2 miles.
And the fly travels 0.5 hours x 12 mph = 6 miles.


This makes sense - note that the first boy and the fly have together covered the nine remaining miles between them, 3 + 6 = 9


So far, the fly has travelled a total of 18 miles + 6 miles = 24 miles.


The distance between the two cyclists is now down to
24 - ((9 + 6) + (3 + 2)) = 4 miles

Continuing for a third leg, our tireless fly starts back from the first boy to the second boy.  The second boy is cycling at 4 mph, the fly is travelling at 12 mph.  Closing speed is 16 mph, and distance to cover is just 4 miles.


4 / 16 = 0.25 hours (15 minutes).


First boy covers 0.25 hours x 6 mph = 1.5 miles
Second boy covers 0.25 hours x 4 mph = 1 mile
Fly travels 0.25 hours x 12 mph = 3 miles


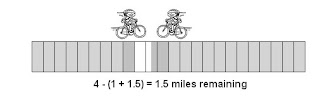
Distance remaining is 24 - (( 9 + 6 ) + (3 + 2) + (1.5 + 1)) = 1.5 miles
Fly has now travelled 18 + 6 + 3 = 27 miles

Clearly, this is going to take a long time to solve through this method.


Here's the shorter way.


The boys have to cover 24 miles.  The first boy cycles at 6 mph, and the second boy at 4 mph.  This means that they are approaching each other with a closing speed of 10 mph, and it will take them 24 miles / 10 mph = 2.4 hours (2 hours and 24 minutes) to complete their journey and meet up. Obviously, there are many different versions of this story, involving trains and so on, but the principle is the same (and you can change the numbers to make them more realistic - I think my boys are pedalling at walking speed!).


The fly, meanwhile, is flying at 12 mph.  This means that in the 2.4 hours it takes the boys to meet, it will fly 2.4 hrs x 12 mph = 28.8 miles.


It really is that easy.  No diagrams, no long complicated adding up then adding up some more.  Sometimes, all that's needed to solve a problem is a different perspective!